
If all the vectors in ?V^\perp? are orthogonal to all the vectors in ?V?, then all the vectors in ?V? will be orthogonal to all the vectors in ?V^\perp?, so the orthogonal complement of ?V^\perp? will be ?V?. So if ?V^\perp? is the orthogonal complement of ?V?, then Definition: Given a subspace H H of Rn R n, the orthogonal complement of H H is the set of vectors in Rn R n, each of which is orthogonal to every vector.

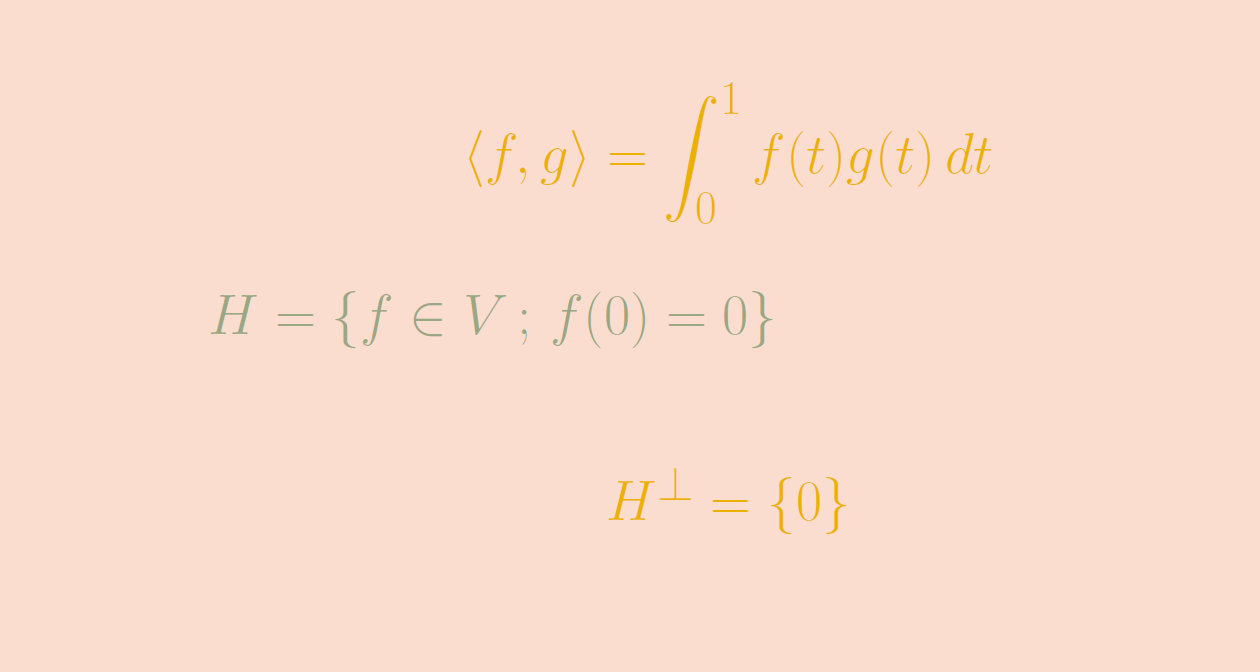
In the same way that transposing a transpose gets you back to the original matrix, ?(A^T)^T=A?, the orthogonal complement of the orthogonal complement is the original subspace. If a set of vectors ?V? is a subspace of ?\mathbb? is closed under scalar multiplication. With a refresher on orthogonality out of the way, let’s talk about the orthogonal complement. Hence, an affine subspace is obtained from a vector subspace by translation.

So to capture the same idea, but for higher dimensions, we use the word “orthogonal” instead of “perpendicular.” So two vectors (or planes, etc.) can be orthogonal to one another in three-dimensional or ?n?-dimensional space. Since by definition rad(V ) is orthogonal to all of V, any complementary subspace W to rad(V ) in the sense of usual linear algebra will give rise to an. (1) (2) or a plane, formed by the solutions of a linear equation (3) These are not necessarily subspaces of the vector space, unless is the origin, or the equations are homogeneous, which means that the line and the plane pass through the origin. This idea of “perpendicular” gets a little fuzzy when we try to transition it into three-dimensional space or ?n?-dimensional space, but the same idea still does exist in higher dimensions.


 0 kommentar(er)
0 kommentar(er)
